New smartphones
Wiko™ is an international brand born in Marseille, France, and is now present in more than 30 countries in Europe, Africa, the Middle East, Asia, and now in the United States. Wiko successfully maintains the top four mobile device position in Western Europe and continues its growth and success.
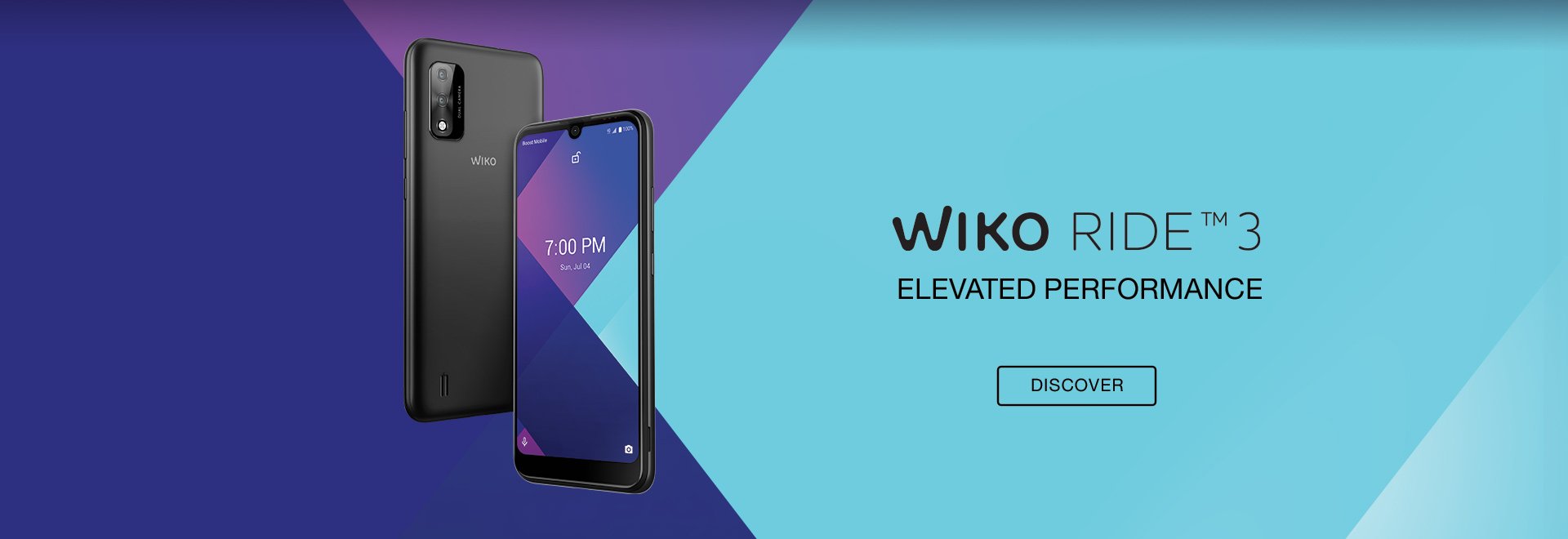
Wiko USA launched in 2019 and debuted its first smartphone with the exclusive partnership of Boost Mobile. The stylish Wiko Ride smartphone is equipped with essential functionalities, affordable, and easy to use.
Wiko USA's vision is to see our consumers as our community that lives on their terms and driven by their individuality. With well-designed technology and beautifully crafted devices, it's easy to explore affordable possibilities to get back to your passion.
Let’s live it.
News

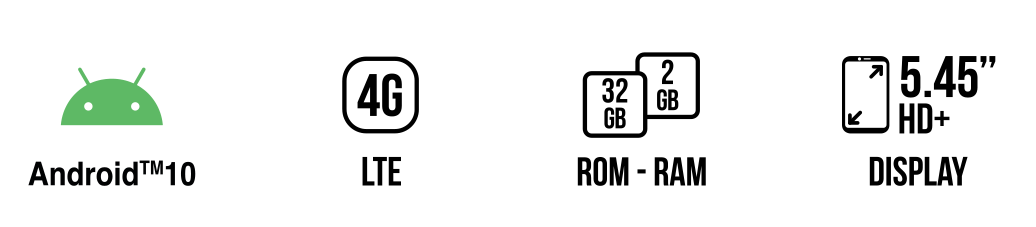
WIKO RIDE™ 2. ABSOLUTE AGILITY
The WIKO RIDE™ 2 upgrades come with an HD+ display, flash on both front and rear cameras, and a quad-core processor for an enhanced performance you're...

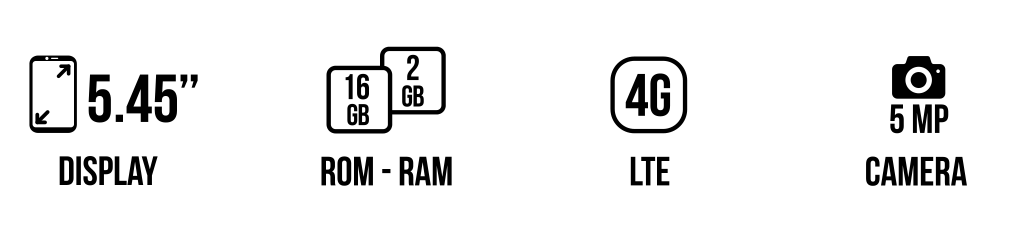
WIKO RIDE™. Simply essential.
Wiko Ride™ comes with 4G speed giving you a smooth internet browsing experience and a 5.45" display to view your favorite content. Learn more about:...

Who is Wiko?
Discover what’s new with Wiko’s Smartphone in 2019! At Wiko, we see life through the eyes of our consumers. Our ambition is to support them to live...
July 2020
Today announced the launch of its new WIKO RIDE™ 2– an upgraded version of the popular Wiko RIDE™ that debuted in the U.S. in 2019 – now available exclusively from Boost Mobile.